¡¡A disfrutar de la geometría!!

CLASE PRIMERA: PRESENTACIÓN Y POLÍGONOS
(Martes, día 2 de mayo)
Hoy hemos aprendido qué es un polígono utilizando los mecanos y hemos llegado a la siguiente definición:
"Un polígono es una figura plana formada por una línea recta cerrada y la superficie que delimita."
 |
| Sí es un polígono. |
 |
| No es un polígono. |
Después, hemos investigado las diferencias que hay entre los polígonos. Para esto, hemos utilizado unos "geoplanos" en los que había dibujados dos hexágonos...
¿Por qué estos dos hexágonos no son iguales?¿Qué les diferencia?
 |
| Polígono irregular. |
 |
| Polígono regular. |
¡Exacto! La diferencia es que uno es un polígono regular y otro es un polígono irregular:
"Un polígono es regular si todos sus lados y ángulos son iguales entre sí."
Por último, utilizando la realidad aumentada, hemos repasado el nombre de todos los polígonos. Desde los que tienen tres lados, hasta los que tienen diez:
(-Añadiré varias fotos de vuestro trabajo el próximo día-)
SEGUNDA CLASE: LOS TRIÁNGULOS
(Jueves, 4 de mayo)
Hoy hemos aprendido muchas curiosidades sobre los triángulos...
En primer lugar, descubrimos que TODOS los triángulos del mundo suman 180º si juntamos todos sus ángulos.
¡Podéis hacer la prueba en vuestra casa! Ahí va un vídeo:
Después de esto estudiamos los tipos de triángulos que existen y, después de jugar un poco, aquí os dejo el resumen de todos ellos:
 |
| (No es necesario que memoricéis cada triángulo. Tan sólo tenéis que conocer sus nombres y características para, dado el caso, podáis identificar alguno otro triángulo.) |
CLASE TERCERA: LOS CUADRILÁTEROS
(Viernes, 5 de mayo)
Hoy hemos conocido otro tipo de polígonos: los cuadriláteros.
Hemos comenzado la clase investigando sobre cómo están formados los cuadriláteros... ¡Y hemos conseguido dividir TODOS los cuadriláteros que formábamos en dos triángulos!
 |
| Cuadrilátero |
 |
| Mismo cuadrilátero dividido en triángulos |
Con esto hemos llegado a la siguiente conclusión:
"Todos los cuadriláteros se pueden dividir en dos triángulos. Por esta razón, la suma de los ángulos de TODOS los cuadriláteros es 360º."
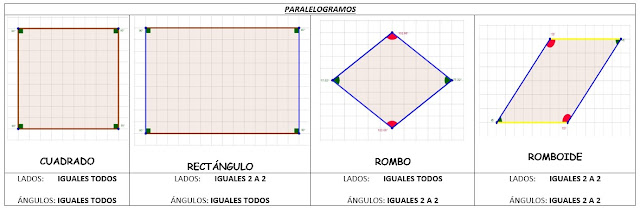
Una vez hemos llegado a este acuerdo, hemos aprendido las diferencias entre los diferentes cuadriláteros: paralelogramos y no paralelogramos.
*Recordad: Los paralelogramos tienen sus cuatro lados paralelos dos a dos.
Los no paralelogramos no tienen sus cuatro lados paralelos dos a dos.
CLASE CUARTA: EL PERÍMETRO
(Lunes, 8 de mayo)
Hoy hemos aprendido el concepto de "perímetro". Como ya sabéis, el perímetro es la SUMA de todos los lados de un polígono. A continuación, tenéis una imagen del perímetro de un cuadrado:
Como era una cosa tan fácil, que ya habíamos visto otros años, nos aventuramos a realizar una serie de problemas, ahí van:
CLASES QUINTA Y SEXTA: DEL PERÍMETRO AL ÁREA Y FÓRMULAS.
(Martes y jueves, 9 y 11 de mayo)
Durante estas dos clases hemos aprendido la diferencia entre lo que es el área de un polígono y el perímetro. Para conseguirlo, hemos formado un cuadrado gigante de 1m^2.
-Añadiré una foto de él-
Aquí os dejo en forma de resumen lo que hemos aprendido:
-Añadiré una foto de él-
Aquí os dejo en forma de resumen lo que hemos aprendido:
Hasta aquí hemos llegado muy bien, ya que ahora... ¡Somos capaces de averiguar el perímetro de cualquier polígono!
Sin embargo, no sucede lo mismo con las áreas... ¿Cómo podemos hacer para poder averiguar el área de cada polígono?
¡Pues hemos investigado entre nosotros para averiguar las fórmulas!
Para empezar, una cosa hemos tenido clara... El área del cuadrado y el área del rectángulo:
Cuadrado:
Rectángulo:
A partir de aquí, tan solo hemos tenido que pensar un poco. Para eso, hemos tenido que seguir unas pistas...
Triángulo:
PISTA:
(Haz "click" en la imagen para verla en movimiento)
FÓRMULA FINAL:
Romboide
PISTA:
FÓRMULA FINAL:
Rombo
PISTA:
(Haz "click" en la imagen para verla en movimiento)
(Viernes, 12 de mayo)
Con todo lo que hemos aprendido hasta ahora, todavía no somos capaces de calcular las áreas de todos los polígonos que hemos estudiado... Por ello, hoy nos hemos centrado en los polígonos regulares.
¡¡Investigando por grupos hemos descubierto una fórmula que nos sirve para cualquier polígono regular!!
Una vez que vimos las pistas, muchos grupos dieron con una posible solución, aquí van un par de ejemplos:
Base x Altura (h) x Nº de lados
2
**Cuidado, no es del todo correcta
2
**Cuidado, no es del todo correcta
"En realidad es muy fácil, consiste tan solo en calcular el área de un triángulo y multiplicarlo por el número de triángulos que hay."
Por una parte, no les falta razón a nuestros compañeros, utilizando ese método podrán averiguar el área de los polígonos regulares. Sin embargo, nosotros queremos ser más profesionales:
Debemos saber que cuando dividimos un polígono regular en triángulos, no existe la "altura", sino que ese segmento recibe el nombre de APOTEMA:
Dentro de un polígono regular: En un triángulo por sí solo:
Apotema Altura (h)
Por lo tanto, si seguimos la fórmula a la que hemos llegado antes gracias a las pistas, deberíamos cambiarle algunas cosas:
BASE (b) x APOTEMA (ap) x Nº de lados
2
2
¡¡¡Ahora sí!!! Ya tenemos una fórmula que funciona para TODOS los polígonos regulares.
Pero... ¡Todavía podemos ser más profesionales! Pensemos...
¿Qué ocurre si multiplicamos la base del triángulo por el número de lados del polígono?
Si multiplicamos la base, es decir, un lado del polígono, por el número total de lados...
¡Estamos calculando el perímetro!
Si hacemos esto, la fórmula final quedaría así:
Perímetro x Apotema
___________________
2
FÓRMULA FINAL Y DEFINITIVA PARA CALCULAR EL ÁREA DE POLÍGONOS REGULARES:
 |
| La forma más correcta es la "Opción 2". |
CLASES OCTAVA Y NOVENA: CIRCUNFERENCIAS Y CÍRCULOS
¡Ya hemos aprendido casi todo! De hecho, ya sabemos las características que los polígonos, así como calcular su perímetro y su área... Pero todavía no hemos hablado de los círculos y las circunferencias. ¡Vamos allá!
En primer lugar, la clase comenzó con un vídeo para introducirnos al mundo de los círculos:
El vídeo trataba sobre meteoritos y el cráter que se forma cuando éstos chocan con La Tierra.
Nosotros nos fijamos en el siguiente cráter:
 |
| Cráter Pingualuit. Canadá. La pregunta que nos hicimos fue la siguiente: ¿Cuánto mide la cadena de montañas que rodean el cráter? ¿Cuánto ocupa la superficie del cráter? |
Antes de empezar a investigar una forma para averiguar todo esto, tuvimos que aprender varios aspectos sobre los círculos:
Una vez trabajados estos conceptos, ya estamos listos para descubrir cuánto medía la cadena de montañas del cráter y cuánto ocupa su superficie.
Para ello, vamos a aprender dos cosas:
1. La longitud de la circunferencia
2. Área del círculo
1- LA LONGITUD DE LA CIRCUNFERENCIA
Mueve la línea azul (derecha) y comprueba lo que ocurre.
Efectivamente, después de realizar varias pruebas con distintos objetos, nos dimos cuenta de que si obtenemos la "longitud de la circunferencia" y la dividimos entre el diámetro del círculo, SIEMPRE nos van a resultar 3 trozos y algo...
Señores y señoras, estos "3 y algo" es el número PI (π), que es igual a 3'14.
Longitud de la circunferencia = PI (π)
Diámetro
Ahora bien, el problema es que, normalmente, no existen cuerdas tan largas como para rodear un cráter entero y saber así cuál es la longitud de su circunferencia... ¿Cómo lo podemos calcular?
FÓRMULA FINAL:
Longitud de la circunferencia = 2 x π x r
2- EL ÁREA DEL CÍRCULO
Pulsa en "start the show"
Como podéis comprobar, se puede deshacer un círculo en un triángulo... A partir de aquí es muy fácil, ya que vosotros ya sabéis calcular el área del un triángulo, ¿verdad?
FIN
Como ya sabéis, esto es todo lo que hemos aprendido y ya no vamos a descubrir nada nuevo. El viernes 19 habrá un control... ¡Estad preparados!
Para que sea más fácil, os dejo un esquema con todo lo que hemos ido aprendiendo: